definieren wir
einen Computer als eine partiell rekursive Funktion
Rainhard Steindl
Dezember 1997
Von der Mathematik als exakteste aller Wissenschaften erwartet man sich klare Antworten auf klare Fragen. Bereits der deutsche Philosoph und Mathematiker G. W. Leibnitz [7] brachte zum Ausdruck, was auch heute noch viele Wissen-schafter unterstreichen würden:
[Mathematik ...], eines Gegenstandes, in dessen Bereich die Wahrheit ohne Mühe und ohne umständliche Experimente so sichtbar gemacht werden kann, daß kein Zweifel übrigbleibt. Es offenbart sich so eine gewisse Reihe, sozusagen eine Richtschnur des Denkens, die uns nicht nur des bereits Gefundenen versichert, sondern uns auch einen zweifelsfreien Weg zu künftigen Erkentnissen weist.Doch schon in den 30er Jahren zeigten die Arbeiten von Gödel, Church, Turing und anderen, daß es auch in der Mathematik Grenzen gibt. Gregory Chaitin konnte sogar zeigen, daß der reine Zufall sogar in der Mathematik zu finden ist.
Wir benötigen für unsere weiteren Untersuchungen eine formale Definition
eines Computers. Ausgehend vom binären Alphabet definieren wir
einen Computer als eine partiell rekursive Funktion
mit der Einschränkung, daß, wenn C (u, v) definiert ist, und u ein echtes Präfix von u' ist, so ist C (u', v) nicht definiert. Mit anderen Worten, die Wertemenge von C ist präfixfrei. u kann als das Programm und v als die Daten für den Computer C angesehen werden. Ein Computer U ist nun universell, wenn es für jeden Computer C (u, v), der konvergiert, eine Konstante sim (C) gibt, mit
wobei |v| die Länge eines Wortes v bezeichnet.
Die Komplexität eines Wortes 
ist definiert als
wobei 
der leere Input ist. Wir schreiben kurz 
. Mit
anderen Worten, die Komplexität eines
Wortes w ist die Länge des kürzesten Programmes, das dieses Wort auf einem
Computer mit leerem Input erzeugen kann. Erweitert man nun diese Definition
bekommt man die bedingte Komplexität eines Wortes
d.h. die Länge des kürzesten Programmes, das mit Input t das Wort w erzeugt. Es ist leicht zu sehen, daß
gilt. Gibt es nun Worte, für die es kein Programm gibt, das wesentlich kürzer ist, als das Wort selbst?
Die Sequenz
ist nicht sehr kompliziert, es läßt sich leicht ein kurzes Programm finden. Gibt es aber für diese Sequenz
ein kürzeres Programm? Eine wichtige Voraussetzung für zufällige Sequenzen ist die Normalität. Eine Folge heißt dann und nur dann normal, wenn jede Ziffer und jeder Block beliebiger Länge von solchen Ziffern mit gleicher asymptotischer Häufigkeit vorkommt. So ist zum Beispiel Champerownes Zahl
normal. Aber nach unserer Intuition ist diese Zahl weit davon entfernt
zufällig zu sein. Und tatsächlich, die Normalität einer Zahl oder einer
Sequenz garantiert noch nicht deren Zufälligkeit.
So gibt es für die Erzeugung von 
(die Normalität von ist zwar
nicht bewiesen, doch wird dies allgemein anerkannt) gibt es mehrere Formeln
(d.h. Programme).
Kehren wir wieder zu unserem binären Alphabet
zurück. Für endliche Worte über diesem Alphabet ist Zufälligkeit
nicht genau definierbar, ein Ansatz ist jedoch folgender: Ein Wort w mit
Länge i ist zufällig, wenn 
. Kann man nun abschätzen
wieviele zufällige Worte es gibt? Nehmen wir an, daß jedes Wort von V mit
Länge < i - 20 ein Programm ist, das ein Wort der Länge i
beschreibt. Es gibt nun
Worte der Länge < i - 20. Das Verhältnis von 
und 
beträgt ungefähr 
. Mit anderen Worten, erzeugt man ein Wort
über dem Alphabet V durch Münzenwürfe, so ist die Wahrscheinlichkeit
größer als 0.999999, daß das Wort zufällig ist!
Jetzt kann es ja demnach
auch nicht schwer sein, die Zufälligkeit einer Zahl zu beweisen, wenn es
soviel davon gibt. Das erweist sich jedoch als unmöglich. Genauer gesagt,
jedes formale System T, das sich mit einem Wort der Länge n
beschreiben laßt, kann nur endlich viele Zahlen (mit Länge < n) als
zufällig identifizieren. Der Beweis ist indirekt. Angenommen wir können
die Zufälligkeit eines Wortes w mit 
beweisen. Dann kann man
einen Computer C entwerfen, der alle Beweise von T durchgeht, bis er
auf den richtigen Beweis stößt. Die Beschreibung von C ist ungefähr n
Bits lang, und wir haben daher ein Programm der Länge n gefunden, das w
beschreiben kann ... ein Widerspruch zu der Annahme, daß w zufällig ist.
Dieser Widerspruch ist mit dem Berry Paradoxon vergleichbar
[2]:
Finde die erste positive Zahl, die nicht in weniger als einer Million Worten beschrieben werden kannDie Zufälligkeit einer unendlichen Sequenz B von Ziffern kann im Gegensatz zu endlichen Worten genauer definiert werden. Ist
ein Präfix der Länge i, dann ist die Folge B zufällig, wenn es
eine Konstante A gibt, sodaß für alle i
gilt. Aus der obigen Definition folgt nun für Minimalprogramme:
Wir definieren nun die Wahrscheinlichkeit eines Wortes
(bezüglich eines Computers C) als
d.h. es wird die Länge aller Programme, die w berechnen berücksichtigt.
Wir schreiben wieder kurz 
.
Mit anderen Worten, diese Zahl gibt uns die Wahrscheinlichkeit, daß ein
zufällig ausgewähltes Programm u auf dem Computer C das Wort w
erzeugt. Aufgrund der Präfix-Freiheit der Wertemenge von C läßt sich
zeigen, daß 
gilt
(für den Beweis siehe [11]).
Analog zu der Definition der bedingten Komplexität definieren wir
als bedingte Wahrscheinlichkeit. Intuitiv ist das also die Wahrscheinlichkeit, daß bei gegebenen Input t ein zufällig gewähltes Programm w erzeugt. Erweitert man nun diese Definition kommt man zu der Anhaltewahrscheinlichlkeit des universellen Computers U
Diese Zahl gibt also an, wie groß die Wahrscheinlichkeit für ein zufällig gewähltes Programm ist, auf einem universellen Computer anzuhalten.
Sei nun 
die binäre Darstellung von 
(die 
heißen auch Magic Bits),
so definieren wir die rationale Zahl 
Betrachten wir nun eine total rekursive Injektion g auf die Wertemenge
von 
. g liefert uns also eine Aufzählung aller möglichen
Programme. Wir können nun so eine Annäherung an definieren
Es ist leicht zu sehen, daß die Folge 
monoton
steigend ist und gegen konvergiert. Der Unterschied zur Definition
von ist der, daß wir hier die einzelnen Programme u mit 
(z.B. ihrer Länge nach) beschriftet haben.
Theorem 1: Gilt 
, so gilt
Der Beweis ergibt sich aus der Ungleichung
Theorem 2: Wissen wir für ein beliebiges i die ersten i Bits von
, können wir das Halteproblem für alle Programme mit Länge < i
entscheiden.
Beweis: Angenommen also wir kennen 
, dann können wir die Zahlen
berechnen, bis wir ein n gefunden haben, sodaß
gilt.
Sei 
nun ein Wort der Länge 
über V. Die Behauptung ist
nun: Ist 
definiert 
ist
eines der Wörter aus 
. Der 
Teil ist klar. Für
den 
Teil gehen wir vom Gegenteil aus: Sei 
, mit
m > n. Daraus ergibt sich aber ein Widerspruch:
Eine erstaunliche Eigenschaft - wenn unser i für das groß
genug ist, könnten hätten wir ein eindeutiges Verfahren, um bisher
ungelöste
Fragen der Mathematik zu entscheiden (diese Fragen müssen sich aber in einer
Länge von 
darstellen), z.B.:
kennen würden, müßten wir
die Busy Beaver Funktion [1] von i berechnen! Die Busy
Beaver Funktion 
ist die maximale Anzahl von 1, die eine
Turingmaschine mit n Zuständen auf das Band schreiben kann, bevor sie
anhält. Die Werte für 
sind bekannt, für weitere Werte
kennt man bestenfalls untere Schranken (z.B.: 
). Die
Funktion ist nicht berechenbar [8].
Chaitin selbst entwarf ein Lisp Programm für die Berechnung von 
[4]. Kann man nun ein Verfahren finden, daß uns ohne viel
Berechnungsaufwand vielleicht sogar berechnen kann? -
Nein:
Theorem 3: Die Folge ist zufällig.
Beweis: Aus dem Beweis von Theorem 2 ergibt sich
d.h. hat ein Wort w die Komplexität 
, dann hat das dem w
zugeordnete Programm höchstens die Länge i. Weiters betrachten wir die
Funktion 
, die für ein gegebenes 
das kleinste m findet, sodaß
gilt. Ist so ein m gefunden, so ist f(x) das erste Wort, das nicht mehr zu der Menge
gehört. Sei C der Computer, definiert durch 
, nun
gilt
Nach (11) ist aber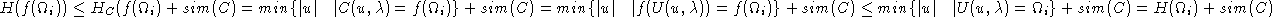
, daher ist
d.h. ist zufällig.
Weiters konstruierte Chaitin eine exponentielle, diophantische Gleichung
mit einem Parameter k, 
, bestehend aus 17000 Variablen.
Eine exponentielle diophantische Gleichung erlaubt im Gegensatz zu einer
herkömm-lichen diophantischen Gleichung ganzzahlige Variable auch im
Exponenten.
Diese so konstruierte Gleichung hat folgende Eigenschaft:
Die k-te Gleichung hat unendliche viele Lösungen, dann
und nur dann, wenn das k-te Bit von 
ist, ansonsten hat sie nur
endlich viele Lösungen. Hier sieht man nun
deutlich die Unlösbarkeit von Hilberts zehntem Problem: Aus (12) ergibt
sich, daß es kein Programm mit Länge 
, das uns sagt, ob die k-te
diophantische Gleichung endlich oder unendlich viele Lösungen hat. Es ist
völlig gleichgültig, für wieviele k wir diese Frage entschieden haben,
dieses Wissen nützt uns gar nichts für die Beantwortung der restlichen
n > k. Wir können uns also die Mühe sparen und eine Münze werfen!
Nachdem wir nun gesehen haben, daß selbst in der Mathematik Zufall herrscht, was bedeutet dies nun für die Mathematik, für die Wissenschaft? Chaitin selbst erwähnt den von Brouwer gegründeten Anschauung einer konstruktivistischen Mathematik [6], die durch seine eigenen Ergebnisse neuen Auftrieb bekommen könnte. Schon heute, gerade mit Hilfe des Computers, wird Mathematik zu einem hohen Maße experimentell betrieben (ganz im Gegensatz zu Leibnitz Zitat aus der Einleitung). Das würde auch den alten Streit beilegen, ob Mathematik eine Naturwissenschaft ist, d.h. Methoden von Theorie und Experiment benötigt. Auch Chaitin schlägt nun vor, Mathematik wie eine Naturwissenschaft zu be-treiben: Mit Experimenten, unbewiesene Annahmen anwenden, wenn sie brauch-bar sind. Schließlich fragt Chaitin [5]
Is there a physical phenomenon that computes something noncomputable? Contrariwise, does Turing's thesis that anything computable can be computed by a Turing machine constrain the physical universe we are in?Roger Penrose etwa behauptet, daß Turingmaschinen (und somit die heute denkbaren Computer) nicht in der Lage sind, menschliche Intelligenz zu erreichen ([9], [10]).
Die geheime Zahl der Weisheit
This document was generated using the LaTeX2HTML translator Version 96.1-e (April 9, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 n-steindl.
The translation was initiated by Wolfgang Slany on Fri Jan 9 19:38:04 MET 1998