A proof of the irrationality
of
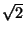
Leslie Lamport
December 1, 1993
Abstract:
Theorem There does not exist 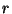 in Q such that
in Q such that 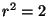 .
.
| |
Proof Sketch: We assume 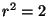 for for 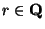 and obtain a contradiction.
Writing and obtain a contradiction.
Writing 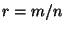 , where , where 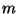 and and 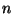 have no common divisors (step
<1>1),
we deduce from have no common divisors (step
<1>1),
we deduce from 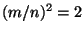 and the lemma that both and the lemma that both 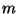 and and 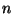 must be divisible by 2 (<1>2 and <1>3).
Assume:
must be divisible by 2 (<1>2 and <1>3).
Assume:
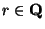
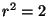
Prove:False
<1>1: Choose 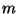 , , 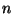 in Z such that in Z such that
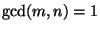
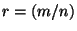
| |
<2>1: Choose 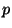 , , 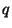 in Z such that in Z such that 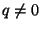 and and 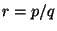 . .
| |
Proof: By assumption <0>:1.
|
Let: 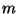
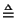 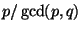
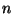
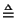 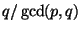
<2>2:
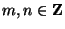
| |
Proof: <2>1 and definition of 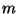 and and 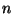 . .
|
<2>3: 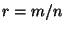
| |
Proof: 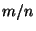 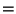 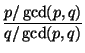 [Definition of [Definition of 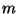 and and 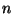 ] ]
= 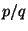 [Simple algebra] [Simple algebra]
= 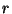 [By <2>1] [By <2>1]
|
<2>4: 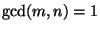 Proof: By the definition of the gcd, it suffices
to:
Assume:
Proof: By the definition of the gcd, it suffices
to:
Assume:
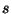 divides divides 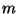
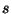 divides divides 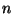
Prove: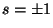
| |
<3>1:
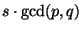 divides divides 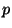 . .
| |
Proof: <2>:1 and the definition of 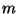 . .
|
<3>2:
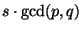 divides divides 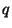 . .
| |
Proof: <2>:2 and definition of 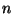 . .
|
<3>3Q.E.D.
| |
Proof: <3>1, <3>2, and the definition of gcd.
|
|
<2>5Q.E.D.
|
<1>2: 2 divides 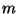 . .
| |
<2>1: 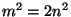
| |
Proof: <1>1.1 implies 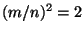 . .
|
<2>2Q.E.D.
| |
Proof: By <2>1 and the lemma.
|
|
<1>3: 2 divides 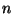 . .
| |
<2>1: Choose 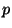 in Z such that in Z such that 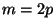 . .
<2>2: 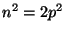
| |
Proof: 2 = 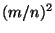 [<1>1.2 and <0>:2] [<1>1.2 and <0>:2]
= 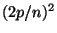 [<2>1] [<2>1]
= 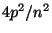 [Algebra] [Algebra]
from which the result follows easily by algebra.
|
<2>3Q.E.D.
| |
Proof: By <2>2 and the lemma.
|
|
<1>4Q.E.D.
|
- 1
- Leslie Lamport, 1993, How to write a proof. In
Global Analysis of Modern Mathematics, pp. 311-321. Publish or
Perish, Houston, Texas, February 1993. A symposium in honor of
Richard Palais' sixtieth birthday (also published as SRC Research
Report 94).
http://research.microsoft.com/users/lamport/proofs/src94.ps.Z
A proof of the irrationality
of
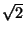
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.56)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html ll1
The translation was initiated by Glowacki Martin / TU Wien Studenten Account Kopie on 2002-10-01
URL of this proof as currently expanded for referencing
and bookmarking purposes.
This HTML file was generated using the pf2html extension, version 0.03.
LaTeX2HTML + pf.sty (hypertext proofs).
Project homepage at http://www.dbai.tuwien.ac.at/proj/pf2html
Glowacki Martin / TU Wien Studenten Account Kopie
2002-10-01
![]() in Q such that
in Q such that ![]() .
.