Wolfgang Slany
http://slany.org/wolfgang/
http://www.dbai.tuwien.ac.at/proj/pf2html/
April 23, 2002
Abstract:
HTML version of a sample
proof
that uses
Lamport's
proof
style
[
1], illustrating how structured proofs can be
converted to
HTML
pages via
LATEX2HTML
enriched with
extensions for Lamport's proof
style. Note that we try
on purpose to carry out Lamport's rule of thumb to ``expand the proof
until the lowest level statements are obvious, and then continue for one
more level'' in order to illustrate the principles of structured
hyper-proofs.
What is the disjunctive normal
form
of
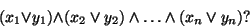
The resulting disjunctive normal form is exponentially blown up
compared to the size of the original conjunctive normal form.
The resulting disjunctive normal form is exponentially blown up
compared to the size of the original conjunctive normal form.
| |
Proof Sketch: Consider the directed graph
shown in Figure 1.
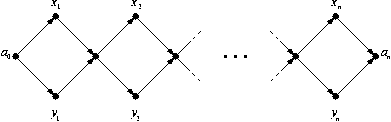 Observe that
paths from
Observe that
paths from 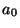 to to 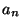 can be described either as going through
nodes ( can be described either as going through
nodes ( 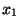 or or 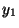 ) and ( ) and ( 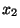 or or 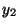 ) and ... and
( ) and ... and
( 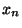 or or 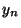 ) (cf. the conjunctive normal form), or
alternatively as going through nodes ( ) (cf. the conjunctive normal form), or
alternatively as going through nodes ( 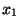 and and 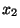 and ... and and ... and
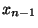 and and 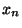 ) or ( ) or ( 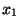 and and 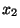 and ... and and ... and 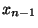 and
and 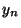 ) or ( ) or ( 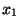 and and 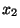 and ... and and ... and 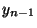 and and 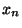 )
or ( )
or ( 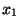 and and 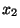 and ... and and ... and 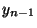 and and 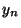 ) or ... or ( ) or ... or ( 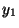 and and 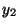 and ... and and ... and 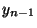 and and 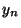 ) (cf. the
disjunctive normal form). The formal proof makes this precise. ) (cf. the
disjunctive normal form). The formal proof makes this precise.
Let: Denote the left side of Equation 2 by
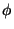 ,
and its right side by ,
and its right side by 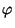 (the variable-names are reused
in Figure 1 to label the top and bottom nodes).
(the variable-names are reused
in Figure 1 to label the top and bottom nodes).
Prove:
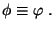
Proof:
1: There is a one-to-one correspondence (a
bijection)
between the
paths from node 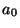 to node to node 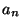 and the minimal satisfying truth
assignments of and the minimal satisfying truth
assignments of 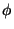 (the conjunctive normal form). (the conjunctive normal form).
| |
1.1: Every path from node 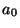 to node to node 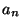 corresponds to a unique minimal satisfying truth assigment of
corresponds to a unique minimal satisfying truth assigment of 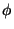 . .
| |
Let:
1.1.1: Let a variable of 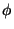 be set to true
whenever the path goes through a node with the same name as the
variable.
Proof: be set to true
whenever the path goes through a node with the same name as the
variable.
Proof:
1.1.2: The truth assignments induced by paths from
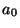 to to 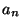 are satisfying truth assigments of are satisfying truth assigments of 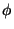 . .
| |
1.1.2.1: Every path from 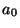 to to 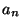 must go through either must go through either 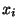 or or
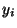 for all for all
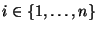 . .
| |
Proof: Structure of the graph in Figure 1.
|
1.1.2.2: Q.E.D.
|
1.1.3: The truth assignments induced by paths from 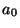 to
to 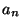 are minimal satisfying truth assigments of are minimal satisfying truth assigments of 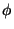 . .
| |
1.1.3.1: Flipping any variable from true to false in
such a truth assignment makes 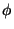 unsatisfied. unsatisfied.
| |
Proof: Structure of 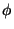 (every conjunct has only one variable
that makes it true in any minimal truth assignment of (every conjunct has only one variable
that makes it true in any minimal truth assignment of
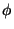 ). ).
|
1.1.3.2: Q.E.D.
|
1.1.4: These minimal satisfying truth assigments are unique.
| |
Proof: 1.1.3, the structure of the graph, the
structure of 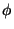 , and because the order of variables in truth
assigments does not matter. , and because the order of variables in truth
assigments does not matter.
|
1.1.5: Q.E.D.
|
1.2: Conversely, every minimal satisfying truth
assignment of 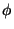 corresponds to a unique path from node corresponds to a unique path from node 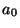 to
node to
node 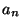 . .
| |
Let:
1.2.1: Let a variable of 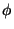 be set to
true whenever the path goes through a node with the same name as
the variable.
Proof: be set to
true whenever the path goes through a node with the same name as
the variable.
Proof:
1.2.2: Every minimal satisfying truth assignment of 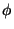 corresponds to a path from node
corresponds to a path from node 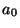 to node to node 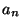 . .
| |
Proof: From the structure of 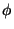 , exactly one variable in each
conjunct must be true in any minimal satisfying truth
assignment of , exactly one variable in each
conjunct must be true in any minimal satisfying truth
assignment of 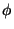 . This defines a path from node . This defines a path from node 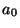 to node to node
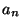 by the structure of the graph in Figure 1 and
1.2.1. by the structure of the graph in Figure 1 and
1.2.1.
|
1.2.3: The thus induced path is unique.
| |
Proof: Structure of 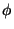 and the construction of the graph in
Figure 1. and the construction of the graph in
Figure 1.
|
1.2.4: Q.E.D.
|
1.3: Q.E.D.
|
2: There is a one-to-one correspondence between
the paths from node 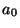 to node to node 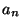 and the minimal satisfying truth
assignments of and the minimal satisfying truth
assignments of 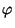 (the disjunctive normal form). (the disjunctive normal form).
| |
2.1: Every path from node 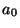 to node to node 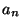 corresponds to a unique minimal satisfying truth assigment of
corresponds to a unique minimal satisfying truth assigment of 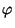 . .
| |
Let:
2.1.1: Let a variable of 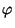 be set to true
whenever the path goes through a node with the same name as the
variable.
Proof: be set to true
whenever the path goes through a node with the same name as the
variable.
Proof:
2.1.2: The truth assignments induced by paths from
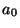 to to 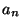 are satisfying truth assigments of are satisfying truth assigments of 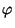 . .
| |
2.1.2.1: Every path from 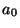 to to 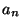 must for all must for all
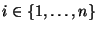 either go through either go through 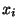 or or 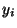 . .
| |
Proof: Structure of the graph in Figure 1.
|
2.1.2.2: Q.E.D.
|
2.1.3: The truth assignments induced by paths from 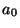 to
to 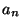 are minimal satisfying truth assigments of are minimal satisfying truth assigments of 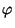 . .
| |
2.1.3.1: Flipping any variable from true to false in
such a truth assignment makes 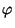 unsatisfied. unsatisfied.
| |
Proof: Structure of 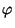 (only one disjunct is made true
by any minimal truth assignment of (only one disjunct is made true
by any minimal truth assignment of 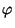 ). ).
|
2.1.3.2: Q.E.D.
|
2.1.4: These minimal satisfying truth assigments are unique.
| |
Proof: 2.1.3, the structure of the graph, the
structure of 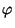 , and because the order of variables in truth
assigments does not matter. , and because the order of variables in truth
assigments does not matter.
|
2.1.5: Q.E.D.
|
2.2: Conversely, every minimal satisfying truth
assignment of 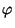 corresponds to a unique path from node corresponds to a unique path from node 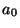 to
node to
node 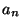 . .
| |
Let:
2.2.1: Let a variable of 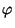 be set to
true whenever the path traverses a node with the same name as
the variable.
Proof: be set to
true whenever the path traverses a node with the same name as
the variable.
Proof:
2.2.2: Every minimal satisfying truth assignment of 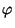 corresponds to a path from node
corresponds to a path from node 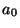 to node to node 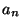 . .
| |
Proof: From the structure of 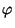 , exactly one variable in each
disjunct must be true in any minimal satisfying truth
assignment of , exactly one variable in each
disjunct must be true in any minimal satisfying truth
assignment of 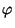 . This defines a path from node . This defines a path from node 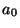 to node to node
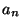 by the structure of the graph in Figure 1 and
2.2.1. by the structure of the graph in Figure 1 and
2.2.1.
|
2.2.3: The thus induced path is unique.
| |
Proof: Structure of 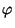 and the construction of the graph in
Figure 1. and the construction of the graph in
Figure 1.
|
2.2.4: Q.E.D.
|
2.3: Q.E.D.
|
3: Q.E.D.
| |
Proof: Since each satisfying truth assignment of a boolean
formula must contain a minimal satisfying truth assignment (by definition
of the latter), and since by proof steps 1 and
2 there must be a one-to-one
correspondence between the minimal satisfying truth assignment of
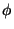 and of and of 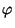 , a truth assignment satisfies , a truth assignment satisfies 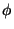 iff
it also satisfies
iff
it also satisfies 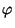 . .
|
|
The help and comments of Marcus Carotta, Wolfgang Goedl, Martina
Osztovits, and Helmut Veith are gratefully acknowledged.
-
- 1
- Leslie Lamport, 1993, How to write a proof. In
Global Analysis of Modern Mathematics, pp. 311-321. Publish or
Perish, Houston, Texas, February 1993. A symposium in honor of
Richard Palais' sixtieth birthday (also published as SRC Research
Report 94).
http://research.microsoft.com/users/lamport/proofs/src94.ps.Z
- 2
- Christos H. Papadimitriou, 1994, Problem
4.4.5. In Computational Complexity, p. 84. Addison-Wesley.
Exponential
blowup
from conjunctive
to disjunctive normal
form
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.56)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html 445
The translation was initiated by Glowacki Martin / TU Wien Studenten Account Kopie on 2002-10-01
URL of this proof as currently expanded for referencing
and bookmarking purposes.
This HTML file was generated using the pf2html extension, version 0.03.
LaTeX2HTML + pf.sty (hypertext proofs).
Project homepage at http://www.dbai.tuwien.ac.at/proj/pf2html
Glowacki Martin / TU Wien Studenten Account Kopie
2002-10-01