FLIP++
Every problem domain needs suitable datatypes and operators to
be done efficiently. StarFLIP++ has the special feature of providing
fuzzy datatypes and operators to effectively deal with real-world
vagueness. Those are defined in FLIP++ together with all instruments
needed for doing defuzzification and inference.
FLIP++ defines a wide range of various operators that are needed
to implement fuzziness. They include:
- fAND (predefined as: truth(x and y) = minimum (truth(x),
truth(y));
- fOR (predefined as: truth(x or y) = maximum (truth(x),
truth(y));
- fNOT (predefined as: truth(NOT X) = 1.0 - truth(x);
With the above operators it is possible to model everything that
is usually done in boolean logic in the same fashion but within
the extended fuzzy-logic domain. As not everyone agrees on how
to define fuzzy operators it is possible to adjust them to ones
own conception.
Together with the predefined operators it is possible to create
new operators that better fit the problem at hand.
In classical set theory a subset A of a set S maps all elements
x of S to the set {0, 1} where 0 means x is not a member of A
while 1 means that x is a member of A.
A fuzzy subset F of a set S maps all elements x of S to the interval
[0..1] with the meaning of 0 and 1 unchanged but values in-between
representing intermediate degrees of membership. This kind of
mapping is usually described by a function called the membership
function (or fuzzy subset) of F.
As membership functions and logic are generalizations of classical
set theory there is no conflict between fuzzy and crisp methods
and it is possible to use them both in the system.
One major advantage of fuzzy logic is that it is usually less
complicated to define membership functions compared with crisp
functions and that they are more intuitively and easier to grasp
(just think of the famous example of the definition of tallness
of a person ...).
In StarFLIP++ you have to define a membership function for every
coinage of a linguistic variable. This can be done in different
ways:
You can define membership functions as shapes with the x-axis
defining the measure (for example temperature) and the y-axis
defining the degree of membership in the interval [0..1]. Commonly
used shapes like triangular or trapezoidal are already present
but again it is possible to define a new, individual shape. The
following pictures show first an example of a single membership
function and then the membership functions for every coinage of
a linguistic variable. As you can see membership functions can
be of different shapes and usually overlap. It is also possible
to mix fuzzy and crisp functions when appropriate.
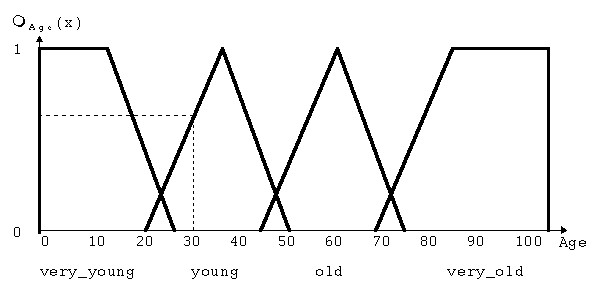
Fig. 1 shows a typical membership function for
the famous age
example. The dashed line indicates that Age=30 belongs to the
linguistic variable young to a degree of 0.7.
The other way to define all membership functions for
a linguistic variable is to define a 6-tuple consisting of support
range (upper end and lower end of the measure) a median its distribution
(around the median) its dilatation (this states the degree of
fuzziness in the interval [0..1] with higher fuzziness nearer
to 1) and its importance (this parameter lies in the [0..1] interval
with higher importances nearer to 1).
(-100, 100, 0, 0.5, 1, 0.9) defines all
membership functions of a linguistic variable with measures in the range
of -100 to 100 a median of 0, a distribution of 0.5 around the
median, fuzziness 1 and an importance of 0.9 ( the importance
belongs of course to the linguistic variable).
Furthermore it is necessary to define the number of coinages for
the linguistic variables and their names.
To actually be able to get something out of the system we need
to specify rules. Rules consist of an antecedent (or premise)
and a conclusion and look like this:
if al_temp is hot and ni_temp is medium then al-ni_heat is acceptable.
al_temp and ni_temp are input variables with hot and medium as
membership functions defined on al_temp and ni_temp, respectively.
Acceptable is a membership function defined on the output variable
al-ni_heat. In the antecedent we determine to what degree the
rule applies while in the conclusion the output variable is assigned
a value. It is also possible that the conclusion consists of more
than one output variable or that there is more than one conclusions
for a rule.
In FLIP++ it is also possible to assign a value in the range of
[0..1] to a rule to state how accurate (and therefor trustworthy)
the rule is
if al_temp is hot and ni_temp is medium then al-ni_heat is acceptable
with accuracy 0.7.
FLIP++ generates the following steps during the inference process:
Fuzzification where the degree of truth for the premise
of each rule is determined for an actual value.
Inference using either max-min or sum-product inferencing.
The first method clips off the membership function of the output
variable(s) at the computed degree of truth for the premise of
the rule (min) and then combines an output fuzzy subset by taking
the pointwise maximum for all the fuzzy subsets assigned to a
variable (max). The second method scales the membership function
of the output variable(s) with the computed degree if truth for
the premise of the rule (product) and then combines an output
fuzzy subset by taking the pointwise sum for all the fuzzy subsets
assigned to a variable (sum).
Defuzzification converts a fuzzy output set to a crisp
number. From the various methods in use FLIP++ uses the CENTROID
method at this time, though it is planned to incorporate other
popular methods as well as allowing the user to introduce own
methods.


(c)1996 Andreas Raggl, Mazen Younes, Markus Bonner, Wolfgang Slany
Last modified: Tue Jun 24 15:42:05 MET-DST 1997
by StarFLIP Team





