The DLV Tutorial

In this tutorial, we give an introduction to Disjunctive Datalog (using some of the extensions of DLV). The tutorial does not give a full description of the usage and capabilities of DLV. For a more complete account of these, see the DLV homepage and the DLV online user manual. The examples shown in this tutorial work with every recent DLV release. Executables of the DLV system for various platforms can be downloaded from the DLV homepage.

The tutorial consists of the following sections, each of them being built around a guiding example:

This page is quite long. People who are in a hurry might appreciate the information that the tutorial is fully on this page, there will be no branches and no links to further pages.

This tutorial is written for computer-literate people with a background different from computer science, or students new to this area. It was originally written for physicists at CERN, and some examples are tailored towards this community.

Introduction

Datalog is a declarative (programming) language. This means that the programmer does not write a program that solves some problem but instead specifies what the solution should look like, and a Datalog inference engine (or Deductive Database System) tries to find the the way to solve the problem and the solution itself. This is done with rules and facts. Facts are the input data, and rules can be used to derive more facts, and hopefully, the solution of the given problem.

Disjunctive datalog is an extension of datalog in which the logical OR expression (the disjunction) is allowed to appear in the rules - this is not allowed in basic datalog.

DLV (= datalog with disjunction) is a powerful though freely available deductive database system. It is based on the declarative programming language datalog, which is known for being a convenient tool for knowledge representation. With its disjunctive extensions, it is well suited for all kinds of nonmonotonic reasoning, including diagnosis and planning.

Finally, we have to mention to the more advanced reader that DLV is relevant to two communities. Firstly, as mentioned, it is a deductive database engine and can therefore be seen as a way to query data from databases which is strictly more powerful than for example SQL (everything that can be done with the core SQL language can also be done with DLV, and more), but it is also often described as a system for answer set programming (ASP). This is a powerful new paradigm from the area of "Nonmonotonic Reasoning" which allows to formulate even very complicated problems in a straightforward and highly declarative way. One may call this paradigm even more declarative than classical logic. Of course, every programming language to be processed by a computer has to have both fixed syntax (i.e. a grammar that specifies what programs of this language have to look like, and what combinations of symbols make a valid program) and semantics (which abstractly specifies what the computer has to do with the program by declaring how a program is to be translated into the/a correct result). There is wide agreement (and also some excitement) that both the syntax and semantics of the language of DLV are very simple and intuitive. In fact, we do not know of any way to make the language even simpler while preserving its characteristics.

Both the syntax and semantics of DLV will be described in this tutorial.

The First Example : Rules and Facts

Suppose we want to model that every time somebody tells us a joke, we laugh. Furthermore, somebody now tells us a joke. This could be done in the following way: 

joke.
laugh :- joke.
The first line is called a fact and expresses that joke is true (a simple word such as joke appearing in a rule or fact which has a truth value is called a proposition. A more general name - which we will use in the following - for the constituents of rules and facts is atom.). The second line is called a rule. It is read as "if joke is true, laugh must also be true". (The sign ":-" is meant to be an arrow to the left, the logic programming version of the implication.)

If the author of such a program decides it appropriate, one can also interpret some causality into a rule and read this one as "from joke follows laugh". This is pure matter of choice of the human, and DLV does not care about it. The left side of a rule is called its head, while the right side is called its body.

A result of a Datalog computation is called a model. The meaning of this is clear: it is a consistent explanation (model) of the world, as far as the Datalog system can derive it. If a datalog program is inconsistent, i.e., it is contradictory, there is simply no model (we will see examples of this later).

Of course, since in this example joke is certainly true (this is given by the fact), laugh is also true. DLV now tries to find all those models of the world that correctly and consistently explain the observations made (= the program). A model assigns a truth value (either true or false) to each atom appearing in the program, and is written as the set of atoms that are true in a certain model. The model of the above program is {joke, laugh}. When all atoms are false in a model, we talk about an empty model (written as {}). Note that having an empty model is very different from finding no model. We will see examples for this later.

Simple datalog programs like the one above always have exactly one model. In general, though, DLV programs may have zero (as mentioned) or even many models. We will see examples of such programs later.

The Second Example : Negation and the Complete World Assumption

Next, suppose we are not aware of being told a joke. In this case, the correct datalog program looks like this: 

laugh :- joke.
The program itself does not express that joke is false, but the so-called Complete World Assumption (CWA) does. It is one of the foundations DLV bases its computations on and says that everything about which nothing is known is assumed to be false. Therefore, the model for this program is {}. (This means that there is a model but it is empty. It is also possible that for a given program there is no model.) We will come back to the CWA in more detail later in the section that discusses DLV as a deductive database system.

Next, we elaborate a bit on this example. First, we want to express that to be able to understand a joke, one has to hear it and must not be stupid. To hear it, one must not be deaf and there must be a joke. Finally, to laugh about the joke, one must understand it. Alternatively, stupid people might laugh without being told a joke. 

joke.
hear_joke :- joke, not deaf.
understand_joke :- hear_joke, not stupid.
laugh :- understand_joke.
laugh :- stupid, not joke.
In two of the rules, we encounter negated atoms. These are true if the atoms themselves are false. We also encounter rules that contain more than one atom in the body. In such a case, a body is true if each of the literals are true (a literal is a possibly negated atom). For example, 
hear_joke :- joke, not deaf.
is read as "if joke is true and deaf is false then hear_joke must be true".

The model for this program is {joke, hear_joke, understand_joke, laugh}. Again, by virtue of the CWA, deaf and stupid are assumed to be false - there are no facts making these atoms true and no rules which can derive their truth. Now suppose we remove joke. from the program and add stupid. instead. Then, the resulting model would be {stupid, laugh}.

Please note the following things: (i) Those atoms that are not listed as elements of the models above are not automatically rendered false. Rather, they are unknown. (ii) Suppose the program would look like this: 
stupid.
laugh :- stupid, not joke.
The model of this program is {stupid, laugh}. If we now add the fact joke. we get the model {stupid, joke}, from which the atom laugh got lost. In other words, you may add more information and lose information that could be derived before because of that. Due to this property, the formalism of DLV is called nonmonotonic, just as mathematical functions which are neither monotonically increasing nor decreasing are called nonmonotonic. At first sight, this may look like an ugly property of this formalism, but in fact, it allows to do many useful things.

The Family Tree Example : Predicates, Variables, and Recursion

So far we have studied simple atoms as the building blocks of our rules. In fact, atoms may be constructed to hold a number of arguments - they are then also called predicates.

In the following program, we have two binary predicates, parent and grandparent. (They are called binary because they both have two arguments.)

We have to map some semantics to the two arguments of the predicates. Here, the first argument is assumed to be the older person (the parent or grandparent), while the second argument refers to the younger person (the child or grandchild). Certainly, we could do it the other way as well, but then we would have to adjust all the rules that will follow. 

parent(john, james).
parent(james, bill).
grandparent(john, bill) :- parent(john, james), parent(james, bill).
Of course, the model of this program is {parent(john, james), parent(james, bill), grandparent(john,bill)}.

With predicates, it is allowed to use variables, which begin with an upper-case character, differently from the constants of the previous program that begin with a lower-case letter. The following program has the same model as the previous example: 

parent(john, james).
parent(james, bill).
grandparent(X, Y) :- parent(X, Z), parent(Z, Y).
This new grandparent rule which uses variables simply models that every parent of a parent is a grandparent.

Note that the facts of a program are often called the Extensional Database (EDB), while the remaining rules are called the Intensional Database (IDB). With DLV, the EDB can be read either from a relational or object-oriented database, or just simply from files, where no separation of rules and facts is required.

We can now extend this example a bit to show how DLV can be used to model knowledge as datalog rules and exploit it. First we add a few more facts to add more people and to express their gender: 

parent(william, john).
parent(john, james).
parent(james, bill).
parent(sue, bill).
parent(james, carol).
parent(sue, carol).

male(john).
male(james).
female(sue).
male(bill).
female(carol).
Then we can add more rules that model family relationships. 
grandparent(X, Y) :- parent(X, Z), parent(Z, Y).
father(X, Y) :- parent(X, Y), male(X).
mother(X, Y) :- parent(X, Y), female(X).
brother(X, Y) :- parent(P, X), parent(P, Y), male(X), X != Y.
sister(X, Y)  :- parent(P, X), parent(P, Y), female(X), X != Y.
The rules for brother and sister use X != Y to require that X and Y are different (one cannot be his own brother). This is called a built-in predicate, since it could be written as something like not_equal(X, Y). DLV knows quite a few of these built-in predicates. For this program, DLV finds the following model (to simplify readability, the facts already listed above were removed from the model below; of course, they still belong there): 
{grandparent(william,james), grandparent(john,bill), grandparent(john,carol),
father(john,james), father(james,bill), father(james,carol),
mother(sue,bill), mother(sue,carol),
brother(bill,carol), sister(carol,bill)}
Let us now exchange the IDB rules against the following (the EDB facts remain the same): 
ancestor(X, Y) :- parent(X, Y).
ancestor(X, Y) :- parent(X, Z), ancestor(Z, Y).
These rules are interesting, since they use recursion to implement transitivity. They express that, to start with, every parent is an ancestor, and, secondly, that every parent of an ancestor is an ancestor. Please note that the semantics used ensures that it is impossible that there be any problems with left-recursion as they occur in languages as Prolog. In DLV, the programmer can safely ignore such considerations.

The model of this program combined with the six-entries parent facts base above results in the following model (where the parent facts were again removed for readability): 

{ancestor(william,john), ancestor(william,james), ancestor(william,bill),
ancestor(william,carol), ancestor(john,james), ancestor(john,bill),
ancestor(john,carol), ancestor(james,bill), ancestor(james,carol),
ancestor(sue,bill), ancestor(sue,carol)}

Finally, some subtle detail has to be noted which is quite useful to improve the readability of the rules. In the case that a certain argument of a predicate is irrelevant for a certain rule, no dummy variable has to be inserted, but the _ can be used. For instance, suppose we want to derive the persons from the parent facts. For this, we can write the following rules: 

person(X) :- parent(X, _).
person(X) :- parent(_, X).

Finally, please avoid calling a predicate as shown in this section a proposition. (It is fine to call them atoms.)

DLV as a Deductive Database System; Comparison Operators

When you use the CWA in one of your programs, you basically view the DLV system as a deductive database system, since you do not ask for what is logically right, but what you can usefully derive from your facts base. Following this approach, you can perform queries on the existing data (the facts base), derive (and "store") new data using queries(=rules), which again can be used to deduce even more data, and, using the CWA, even ask queries as to what is not in (or derivable from) your database.

Consider the following example in SQL in the well know business domain (which many relational database systems examples use). Emp is a relational table containing employee information, and dept contains data on departmens of a company in which the employees work. 
SELECT e.name, e.salary, d.location
FROM   emp e, dept d
WHERE  e.dept = d.dept_id
AND    e.salary > 31000;
When the relational tables are encoded as a facts base, we can rewrite the above query into a datalog rule: 
emp("Jones",   30000, 35, "Accounting").
emp("Miller",  38000, 29, "Marketing").
emp("Koch",  2000000, 24, "IT").
emp("Nguyen",  35000, 42, "Marketing").
emp("Gruber",  32000, 39, "IT").

dept("IT",         "Atlanta").
dept("Marketing",  "New York").
dept("Accounting", "Los Angeles").

q1(Ename, Esalary, Dlocation) :- emp(Ename, Esalary, _, D), dept(D, Dlocation),
   Esalary > 31000.

As you can see, joins are achieved via variable binding (we use the same variable D both in emp and in dept), selections can for example be achieved by the comparison operators, and projections (i.e. where unwanted data columns are excluded from a query result) can be accomplished by using _ or an unbound variable.

You can use DLV to ask all the queries that are possible in the core SQL language. Furthermore, (as you will see when the full expressive power of DLV is unveiled later in this tutorial) you can also encode many useful queries that cannot be expressed in SQL.

This example used another feature of DLV that has not been introduced yet: comparison operators. DLV supports the operators <, >, >=, <=, and = for integers, floating point values, and strings. This is an extension that is not part of basic datalog, but it is convenient and also compatible with the philosophy of datalog, as you can think of an expression X > Y as a predicate greater_than(X,Y) for which the facts base of all the greater-than relationships between constant symbols in your program are automatically generated. Therefore, we call these comparison operators built-in predicates.

Note that you could also rewrite q1 to use the operator = for the join. The rule below obtains the same result as the one shown earlier: 

q1(Ename, Esalary, Dlocation) :- emp(Ename, Esalary, _, D1),
                                 dept(D2, Dlocation), D1 = D2,
                                 Esalary > 31000.

Download example program.

The Railway Crossing Example : True Negation and Negation as Finite Failure

DLV supports two kinds of negation. Here, we emphasize the difference between explicitly expressing the falseness of an atom and having it done by the Complete World Assumption. The following program uses the CWA. It has the model {cross} because train_approaching is assumed to be false (as it being true is not stated anywhere). This kind of negation is called negation as (finite) failure or naf. 

cross :- not train_approaching.
The next program uses so-called true or classical negation. Since -train_approaching is not known to be true, the following program has only an empty model. 
cross :- -train_approaching.
The difference between the two kinds of negation is quite important: In the first example, we cross the railroad track if we have no information on any trains approaching, which is quite dangerous, while in the second example, we only cross if we know for sure that no train comes. In particular, the left side of the previous rule will only be true if 
-train_approaching.
is in the facts base of the program.

True negation is stronger than negation as finite failure. If something is true via true negation, it is always also true if negated by negation as finite failure. For example, the program 

cross :- not train_approaching.
-train_approaching.
has the model {cross, -train_approaching}.

Using True Negation also allows to build programs that are contradictory and have no models. Consider the following example: 

cross.
-cross.
Certainly, this program cannot have a model. This is very different from a program that has an empty model, which would just mean that the program represents a possible situation but that all of its atoms are assumed to be false.

The Broken Arm Example : Disjunctive Datalog and the Stable Model Semantics

Suppose you have met a friend recently and you know that he had one of his arms broken, but you don't know which one. Now you didn't receive a greeting card for your birthday and wonder if you should be angry on him or if he just cannot write because of his broken arm. Finally, you know that he writes with his right hand. The following DLV program computes the two possible explanations for the observations you made. 
left_arm_broken v right_arm_broken.
can_write :- left_arm_broken.
be_angry :- can_write.
The first rule is called a disjunctive rule; The v is read as "or" and the whole rule is read as "For sure, either the left or the right arm is broken." As we can see here, a disjunctive rule may (but does not have to) have an empty body (= lack a body). It is still called a rule, since it is certainly not a fact. (It is unknown if the left or the right arm is broken.)

Being able to process incomplete information (i.e. being unsure if the left or the right arm is broken) is one of the great strengths of DLV. The resulting models of this query are {left_arm_broken, can_write, be_angry} and {right_arm_broken}.

In fact, the disjunction left_arm_broken v right_arm_broken. also allows both left_arm_broken and right_arm_broken to be true at the same time. Still, DLV does not output the model {left_arm_broken, right_arm_broken, can_write, be_angry} due to the computing paradigm that it uses to cope with uncertainty, and which is called the Stable Model Semantics. Under this semantics, a model is not stable if there is a smaller model which is a subset of it (which is the case for both stable models shown above with respect to the "big" model containing left_arm_broken and right_arm_broken). While this might seem complicated, it is a very powerful feature of DLV which is very useful for all kinds of reasoning. We will come back to this later in this tutorial. (For the moment, we want to emphasize that this one "big" model which is not stable would be obviously wrong in this application.)

Note that the same uncertainty can also be expressed by the following program: 

left_arm_broken :- not right_arm_broken.
right_arm_broken :- not left_arm_broken.
can_write :- left_arm_broken.
be_angry :- can_write.

This program results in the same pair of models. The method used here is called Unstratified Negation and is considered less elegant than the first method. Also, there are certain interesting reasoning problems that DLV can solve and which can only be expressed with true disjunction but not with unstratified negation.

Finally, please note that rule bodies may either contain positive (nonnegated) atoms, atoms negated by true negation, and atoms negated by negation as failure, while rule heads may only contain positive atoms and true negation, but no negation as failure. In other words, a rule such as 

not a :- b.   % INVALID !!!
is not valid! (The % sign in a DLV program starts a comment which goes to the right to the end of the line.)

Strong Constraints

DLV also supports integrity constraints (strong constraints). A constraint is a rule with an empty head. If its body is true (which is of course the case exactly if all the literals in the body are true at the same time), a model is made inconsistent and is removed. For example, in the family tree example which was presented earlier, we can easily write an integrity constraint to assure that the facts base does not erroneously contain contradicting facts saying that a person is male and female at the same time. 

:- male(X), female(X).
This kind of constraints is called strong constraints because there is also a different kind (weak constraints) supported by DLV which is not addressed in this tutorial. This other kind of constraints is very useful to solve optimization problems.

Graph Coloring: Guess&Check Programming

Graph 3-colorability is a hard (NP-complete) problem. It is the problem of deciding if there exists a coloring of a map of countries corresponding to the given graph using no more than three colors in which no two neighbour countries (nodes connected by an arc) have the same color. It is known that every map can be colored given these constraints if four colors are available. 

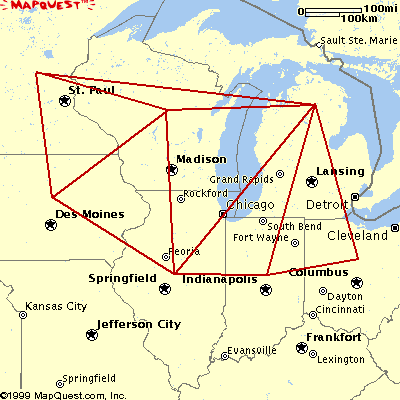
node(minnesota).
node(wisconsin).
node(illinois).
node(iowa).
node(indiana).
node(michigan).
node(ohio).

arc(minnesota, wisconsin).
arc(illinois, iowa).
arc(illinois, michigan).
arc(illinois, wisconsin).
arc(illinois, indiana).
arc(indiana, ohio).
arc(michigan, indiana).
arc(michigan, ohio).
arc(michigan, wisconsin).
arc(minnesota, iowa).
arc(wisconsin, iowa).
arc(minnesota, michigan).
This problem can now be solved with a very simple datalog program, in which we first guess a coloring by using a disjunctive rule and then check it by adding a (strong) constraint which deletes all those colorings that do not satisfy our requirements (that there may be no arc between two nodes of equal color): 
% guess coloring
col(Country, red) v col(Country, green) v col(Country, blue) :- node(Country).

% check coloring
:- arc(Country1, Country2), col(Country1, CommonColor), col(Country2, CommonColor).
This problem instance has 6 solutions (stable models), therefore, it is 3-colorable. Below, one solution is shown, in which the facts base has again be removed for better readability: 
{col(minnesota,green), col(wisconsin,red), col(illinois,green),
 col(iowa,blue), col(indiana,red), col(michigan,blue), col(ohio,green)}

This method (guess&check programming) allows to encode a large number of complicated problems in an intuitive way. DLV can then use such an encoding to solve the problems surprisingly efficiently.

Download example program.

As an exercise, you can use DLV to prove that a map of Germany, Belgium, Luxembourg and France is not 3-colorable.

The Fibonacci Example: Built-in Predicates and Integer Arithmetics

Note that this section introduces some features of DLV which are not part of standard datalog.

In the following example, the Fibonacci function is defined, which is relevant in areas as disparate as Chaos Theory and Botanics. Its starts with the following values: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ... (Apart from the first two values, each value is defined as the sum of the previous two.) 

true.
fibonacci(1, 1) :- true.
fibonacci(1, 2) :- true.
fibonacci(F, Index) :- +(F1, F2, F),
                       fibonacci(F1, Index1),
                       fibonacci(F2, Index2),
                       #succ(Index1, Index2),
                       #succ(Index2, Index).
This program uses the built-in predicates + (which adds or subtracts integer numbers) and #succ (the successor function). Note that for better readability, it is also correct to write F = F1 + F2 instead of +(F1, F2, F) and Index2 = Index1 + 1 instead of #succ(Index1, Index2). Still, these simple equations always map to the built-in predicates and may not be extended any further. (It is not allowed to write A = B + C + D, this has to be split into two parts.)

The second topic that has to be discussed at this point is why the fact true. was introduced. The reason for this is the strong separation that is made between EDB and IDB predicates. Since fibonacci is used on the left-hand side of a rule, it is in the IDB. IDB predicates cannot be used in facts (because then they would have to be in the EDB). Because of that, a fact is introduced and rules are built that are always true and are therefore equivalent to facts. Note that this distinction between IDB and EDB predicates is not necessary anymore in the most recent versions of DLV. Therefore, you can now declare fibonacci(1, 1) and fibonacci(1, 2) simply as facts.

Whenever integer arithmetics are used, the range of possible values has to be restricted, since DLV requires the space of possible solutions to be finite. This is done by invoking DLV with the option -N. (For a full description of DLV usage, refer to the DLV manual.) For example, invoking DLV with 

dl -N=100 fibonacci.dl
results in the model 
{true, fibonacci(1,1), fibonacci(1,2), fibonacci(2,3), fibonacci(3,4),
 fibonacci(5,5), fibonacci(8,6), fibonacci(13,7), fibonacci(21,8),
 fibonacci(34,9), fibonacci(55,10), fibonacci(89,11)}
These are all the Fibonacci numbers not greater than 100.

Download example program.


Click here for some interesting material on Fibonacci numbers.

The 8-Queens Example: Guess&Check Programming with Integers

The 8 queens problem asks for a solution in which 8 queens are placed on a 8 x 8 chess board without threatening eachother. A queen threatens another if it is in the same row, column, or on a diagonal. 
% guess horizontal position for each row
q(X,1) v q(X,2) v q(X,3) v q(X,4) v q(X,5) v q(X,6) v q(X, 7) v q(X,8) :- #int(X), X > 0.

% check

% assert that each column may only contain (at most) one queen
:- q(X1,Y), q(X2,Y), X1 <> X2.

% assert that no two queens are in a diagonal from top left to bottom right
:- q(X1,Y1), q(X2,Y2), X2=X1+N, Y2=Y1+N, N > 0.

% assert that no two queens are in a diagonal from top right to bottom left 
:- q(X1,Y1), q(X2,Y2), X2=X1+N, Y1=Y2+N, N > 0.
To run this program with DLV, type the following: 
dl -n=1 -N=8 8queens.dl
This will return a result like 
{q(1,3), q(2,7), q(3,2), q(4,8), q(5,5), q(6,1), q(7,4), q(8,6)}
To get all 92 correct solutions, type 
dl -N=8 8queens.dl

Download example program.

A simple Physics Diagnosis example

We will now show how to use DLV to do diagnosis. We choose a physics application domain, a simplified version of ECAL pre-calibration.
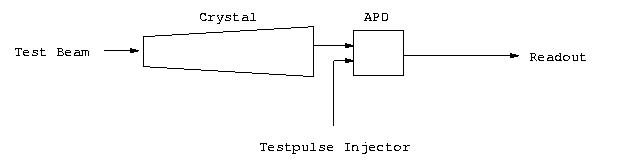
As shown in the picture, a test beam is directed onto a scintillating crystal whose light emission is measured by an avalanche photodiode (APD). The measurement is then read with some readout electronics. Alternatively to the beam reading, the APD can receive a test pulse signal, which allows to check the correct functioning of the APD independently from the crystal. The following program allows to automatically diagnose malfunctioning parts: 
ok(testpulse_reading).
ok(beam_reading).

good(crystal) v bad(crystal).
good(apd) v bad(apd).

:- good(X), bad(X).

good(crystal) :- ok(beam_reading).
good(apd) :-     ok(beam_reading).
bad(apd) v bad(crystal) :- not ok(beam_reading).
good(apd) :-     ok(testpulse_reading).
bad(apd)  :- not ok(testpulse_reading).
The program starts with two facts expressing our observations. Here, both the testpulse reading and the beam reading were found to be correct; below, we will evaluate the program with different observations. The following two rules tell the system that crystals and APDs are either working or broken. After this follows a constraint that assures that they cannot be both at the same time. Finally, there are five rules that are a collection of expert knowledge. They model the knowledge about the domain and show quite clearly why the test pulse is available as a separate input to the APDs: it allows to find out if the APD works correctly without having to make any assumptions about the crystal. If the reaout of the beam on the other hand were not correct, one could not be sure if the responsible part is the crystal or the APD.

Here, the unique result is the model {good(crystal), good(apd)}. Suppose we exchange the two EDB facts (the first two lines of this program) to ok(testpulse_reading). then the result changes to {good(apd), bad(crystal)}. The whole set of different cases is shown in the following table:

EDB Model(s)
{ok(testpulse_reading). ok(beam_reading).} {good(crystal), good(apd)}
{ok(testpulse_reading).} {good(apd), bad(crystal)}
{ok(beam_reading).} no model
{} {bad(apd), good(crystal)},
{bad(apd), bad(crystal)}

The case that the facts base is {ok(beam_reading).} is also interesting: According to our program, if ok(beam_reading) is true, ok(testpulse_reading) also has to be true. Therefore, there is no consistent model in this case. In other words, according to our program, such observations cannot be made.

A different way to implement the Physics Diagnosis example

The way to do diagnosis that was presented in the previous section has two drawbacks: It requires that more knowledge than necessary has to be coded in the program, and resulting from this, the program does not really do anything original. Also, it it hard to extend. Here, we show a different (better) way to do diagnosis in the same application domain. We represent the system as a graph of its units: 
connected(beam, crystal).
connected(crystal, apd).
connected(testpulse_injector, apd).
connected(apd, readout).

good_path(X,Y) :- not bad(X), not bad(Y), connected(X, Y).
good_path(X,Z) :- good_path(X,Y), good_path(Y, Z).

bad(crystal) v bad(apd).

testpulse_readout_ok :- good_path(testpulse_injector, readout).
beam_readout_ok :- good_path(beam, readout).
In this example program, we have left away all the possible observations, which we implement as constraints, as shown in the following table:

Observations (Constraints) Model(s) (good_path predicates omitted)
{} {bad(crystal), testpulse_readout_ok},
{bad(apd)}
{:- testpulse_readout_ok.} {bad(apd)}
{:- beam_readout_ok.} {bad(crystal), testpulse_readout_ok},
{bad(apd)}
{:- beam_readout_ok.
:- testpulse_readout_ok.} 		{bad(apd)}
{:- not testpulse_readout_ok.} {bad(crystal), testpulse_readout_ok}
{:- not beam_readout_ok.} no model
{:- not beam_readout_ok.
:- not testpulse_readout_ok.} 		no model

Download example program.

The Monkey&Banana Example: Planning

The following example shall give an idea of how DLV can be used to do planning.

Please note that there is a DLV planning frontend that uses a convenient special-purpose planning language and which is not described in this tutorial. Instead, we use plain disjunctive datalog for solving planning problems here. If you are interested in this frontend, please refer to the DLV homepage for further information.

Consider the following classic planning problem. A monkey is in a room with a chair and a banana which is fixed to the ceiling. The monkey cannot reach the banana unless it stands on the chair; it is simply too high up. The chair is now at a position different from the place where the banana is hung up, and the monkey itself initially is at again a different place.

Since the program is quite long compared to the earlier examples, it will be explained step by step. 

walk(Time) v move_chair(Time) v ascend(Time) v idle(Time) :- #int(Time).
At each discrete point in time, the monkey performs one of the following for actions: it walks, it moves the chair (while doing this, it also moves through the room), it climbs up the chair, or it does nothing. #int is again a built-in predicate which is true exactly if its argument is an integer value. 
monkey_motion(T) :- walk(T).
monkey_motion(T) :- move_chair(T).

stands_on_chair(T2) :- ascend(T), T2 = T + 1.
:- stands_on_chair(T), ascend(T).
:- stands_on_chair(T), monkey_motion(T).
stands_on_chair(T2) :- stands_on_chair(T), T2 = T + 1.
After climbing up the chair, it is on it. If is is already on it, it cannot climb up any further. While on the chair, it cannot walk around. If it was on the chair earlier, it will be there in the future. 
chair_at_place(X, T2) :- chair_at_place(X, T1), T2 = T1 + 1, not move_chair(T1).
chair_at_place(Pos, T2) :- move_chair(T1), T2 = T1 + 1,
   monkey_at_place(Pos, T2).
If the chair is not moved, it will stay at the same place. If the monkey moves the chair, it changes its position. 
monkey_at_place(monkey_starting_point, T) v
monkey_at_place(chair_starting_point, T) v
monkey_at_place(below_banana, T) :- #int(T).
The monkey is somewhere in the room. (For simplicity, only three positions are possible.) 
:- monkey_at_place(Pos1, T2), monkey_at_place(Pos2, T1),
   T2 = T1 + 1, Pos1 != Pos2, not monkey_motion(T1).

:- monkey_at_place(Pos, T2), monkey_at_place(Pos, T1), T2 = T1 + 1,
   monkey_motion(T1).

:- ascend(T), monkey_at_place(Pos1, T), chair_at_place(Pos2, T), Pos1 != Pos2.

:- move_chair(T), monkey_at_place(Pos1, T), chair_at_place(Pos2, T),
   Pos1 != Pos2.
The monkey cannot change its position without moving. The monkey cannot stay at the same place if it moves. It cannot climb up the chair if it is somewhere else. It cannot move the chair if it is somewhere else. 
monkey_at_place(monkey_starting_point, 0) :- true.
chair_at_place(chair_starting_point, 0) :- true.
true.
Initially, the monkey and the chair are at different positions. 
can_reach_banana :- stands_on_chair(T), chair_at_place(below_banana, T).
eats_banana :- can_reach_banana.
happy :- eats_banana.

:- not happy.
The monkey can only reach the banana if it stands on the chair and the chair is below the banana. If it can reach the banana, it will eat it, and this will make it happy. Our goal is to make the monkey happy. 
step(N, walk, Destination) :- walk(N), monkey_at_place(Destination, N2),
                              N2 = N + 1.
step(N, move_chair, Destination) :- move_chair(N),
                                    monkey_at_place(Destination, N2),
                                    N2 = N + 1.
step(N, ascend, " ") :- ascend(N).
The step rules collect all the things we can derive from the situation and build a consistent plan. (There is no step rule for the action idle since we are not interested in it.)

This program again uses integer arithmetics; to find a plan, the maximum integer variable has to be set to at least 3: 

dl -N=3 banana.dl
This results in the following model (If N is set to a value greater than 3, DLV will find other plans that make the monkey happy.) 
{chair_at_place(chair_starting_point,0),
monkey_at_place(monkey_starting_point,0),
monkey_at_place(chair_starting_point,1),
monkey_at_place(below_banana,2),
monkey_at_place(below_banana,3),
walk(0), move_chair(1), ascend(2), idle(3),
chair_at_place(chair_starting_point,1),
chair_at_place(below_banana,2),
chair_at_place(below_banana,3),
monkey_motion(0), monkey_motion(1),
step(0,walk,chair_starting_point),
step(1,move_chair,below_banana),
step(2,ascend," "),
stands_on_chair(3), can_reach_banana, eats_banana, happy}
Download example program.