|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Shift Design and Break Scheduling Benchmarks |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Benchmark instances for
the shift design and break scheduling problem Validator,
benchmark instances and best known solutions for the shift design and break
scheduling problem can be found here. Benchmark instances for
the supervision personnel break scheduling problem. We
propose two different sets of randomly generated examples for the regarded break
scheduling problem for supervision personnel, which can be used further by
other researchers to compare their results with ours. Set 1 of randomly generated problems (download) These
examples were generated from the first thirty benchmark instances in set 1
for the shift-design
problem. Set 2 of randomly generated problems (download) These
examples were generated from the first thirty benchmark instances in set 2
for the shift-design
problem. Problem settings
for the benchmark instances
The
settings for these instances were obtained from a real-life use case for
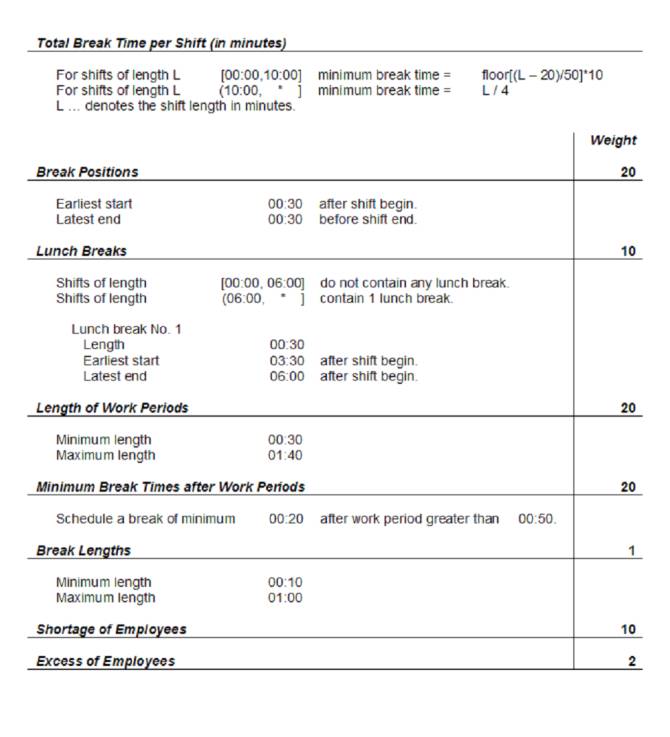
supervision personnel. The following screenshot summarizes how much break
time should be scheduled in each shifts and presents the constraint-settings
for a desired solution.
How are the benchmark instances generated? 1. Generating a shift plan. To
generate a shift plan we considered the randomly generated benchmark instances
for the shift design problem. The shifts are extracted from the sample
solution of each instance and represent the input shift plan for an instance
of the break scheduling problem for supervision personnel. 2. Creating the breaks of each shift. First
of all, for each shift the total amount of break time to be scheduled is
computed. The break time is then distributed among the lunch breaks of
required length and monitor breaks whose durations range between ten or
twenty minutes. Example:
Example:
3. Scheduling breaks in each shift. Breaks
are scheduled within their associated shifts such that the following
constraints satisfy the following constraints of the break scheduling problem
for supervision personnel are satisfied completely: §
C1 Break Positions §
C2 Lunch Breaks §
C3 Length of Work Periods §
C4 Minimum Break Times §
C5 Break Lengths For
that purpose, we formulate a simple temporal constraint satisfaction problem
(STP) [1]. In our formulation the start and end of shifts and breaks are
modelled as variables. The values for minimum and maximum distances and
lengths are encoded as time intervals restricting the relative distances
between variables. The resulting STP is the solved with a randomized version
of Floyd-Warshall’s all-pairs-shortest-path
algorithm [2]. So we finally obtain a shift, which contains the required breaktime and satisfies all the constraint C1
Break Positions, C2 Lunch Breaks, C3 Length of
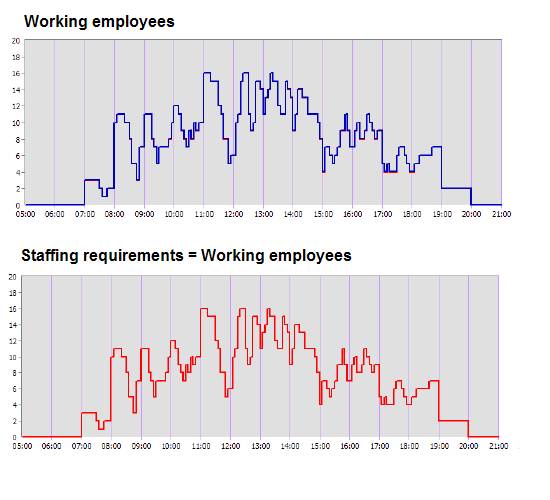
Work Periods, C4 Minimum Break Times and C5 Break Lengths. 5. Determining staffing requirements. Finally,
for each time slot of the planning period the staffing requirements is set to
the number of working employees. In that way we can guarantee that the
resulting problem instance has a solution, which avoids shortage and excess
of employees. Moreover, that solution is able to satisfy all other
constraints.
References [1] Dechter, R., Meiri,
I., and Pearl, J. (1991). Temporal constraint networks. Artif.
Intell., 49(1-3):61–95. [2] Papadimitriou,
C. H. and Steiglitz, K. (1982). Combinatorial
Optimization: Algorithms and Complexity. Prentice-Hall. [3] Andreas
Beer, Johannes Gärtner, Nysret
Musliu, Werner Schafhauser,
Wolfgang Slany. An AI-Based Break-Scheduling System for Supervisory Personnel.
Accepted for publication in IEEE Intelligent Systems. Solutions for this problem from other
researchers Solutions
from Akkermans et al: Solutions
Reference:
Arjan Akkermans, Gerhard Post
and Marc Uetz,
Solving the Shifts and Breaks Design Problem Using Integer Linear
Programming p. 137-152 at Proceedings
of PATAT 2018 (http://patatconference.org/patat2018/proceedings/) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2008 © Database and Artificial Intelligence
Group, Vienna University of Technology
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||